Trigonometry Challenge
You will find in this article a challenging problem of trigonometry. Give it a try, see if you can find the solution !
Short note about trigonometry
Origin of the word: from the Greek trigōnon "triangle" + metron "measure". It is a branch of mathematics dealing with the calculation of triangular shapes and properties of associated angle functions (sinus, cosinus, tangent).
Regarding geometric aspects of trigonometry, various methods are available, some of them known by many and taught at school from year 9 and others more advanced. By increasing order of sophistication:
- Pythagoras’ theorem,
- Basic trigonometric ratios applicable to right triangles (sin, cos, tan),
- Sine rule, cosine rule applicable to any triangle.
The problem
Find the area of the following irregular quadrilateral ABCD where the length of the four sides and one angle are given.
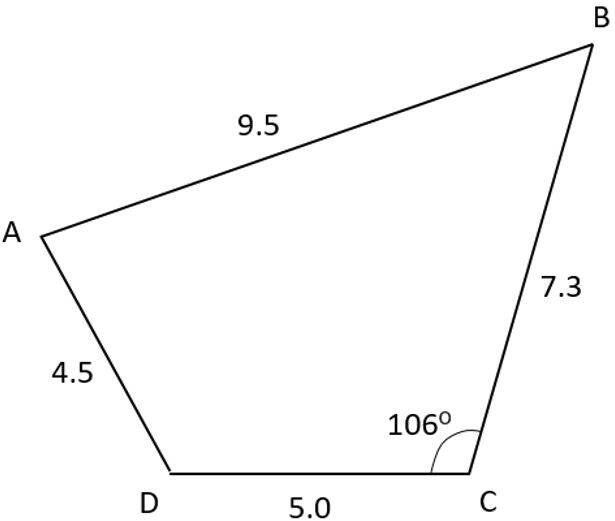
Solution
The following basic techniques are used for the resolution of this problem:
- Application of sin trigonometric ratio
- Formula for the area of any triangle: Area = Base length * height / 2
- Cosine rule: an extension of Pythagoras’ theorem to any triangle which is not necessarily a right triangle: c2 = a2 + b2 – 2ab cos(C)
And of course, as in most trigonometric problems, the solution requires breaking up the geometric figure into manageable triangles.
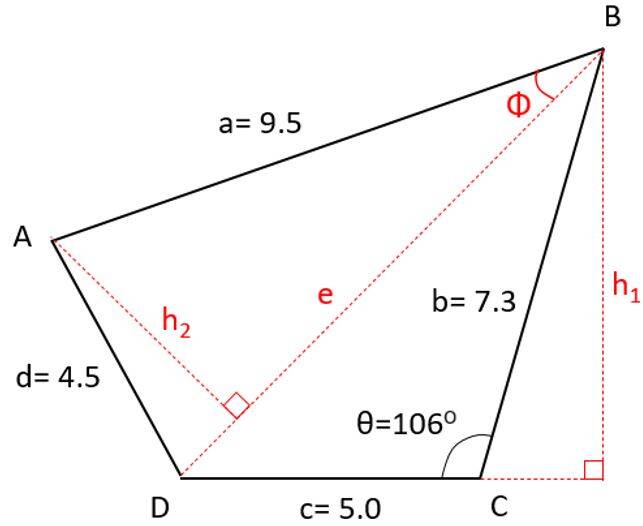
Step 1
Area of BCD triangle: use triangle area formula: A = Base * Height / 2
with: Base = c and Height = b sin (π - θ)
Note: the formula is also applicable in this case of an obtuse triangle ( θ > 90o)
h1 = b sin (π - θ) = 7.02
A1 = c h1 / 2 = 17.54
Step 2
Length of BD diagonal: use Cosine rule
e2 = b2 + c2 - 2 bc cos(θ) = 98.41
e = 9.92
Step 3
Angle Φ: use Cosine rule
d2 = a2 + e2 - 2 ae cos(Φ)
cos(Φ)= (a2 + e2 -d2 ) / (2 ae) = 0.89
Φ =26.68
Step 4
Area of ABD triangle: use triangle area formula A = Base * Height / 2
with: Base = e and Height = a sin (Φ)
h2 = a sin (Φ) = 4.27
A2 = e h2 / 2 = 21.16
Step 5
Total area = A1 + A 2 = 38.70
Maak jouw eigen website met JouwWeb